8.26 Chapter 06

비지도 학습

타깃을 모르는 비지도 학습

• 비지도 학습: 타깃이 없을 때 사용하는 머신러닝 알고리즘

과일 사진 데이터 준비하기

import numpy as np
import matplotlib.pyplot as plt

fruits = np.load('fruits_300.npy')

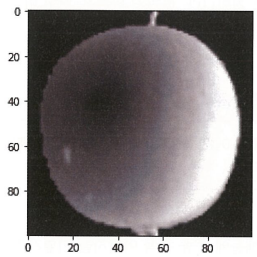
plt.imshow(fruits[0], cmap='gray')
plt.show()

픽셀값 분석하기

• 넘파이 배열을 나눌 때 100 * 100 이미지를 편쳐서 길이가 10,000인 1차원 배열로 만듭니다.

apple = fruits[0:100].reshape(-1, 100*100)
pineapple = fruits[100:200].reshape(-1, 100*100)
banana = fruits[200:300].reshape(-1, 100*100)

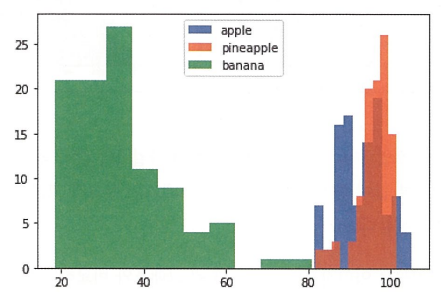
plt.hist(np.mean(apple, axis=1), alpha=0.8)
plt.hist(np.mean(pineapple, axis=1), alpha=0.8)
plt.hist(np.mean(banana, axis=1), alpha=0.8)

plt.legend(['apple', 'pineapple', 'banana'])

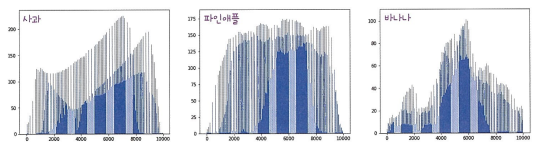
• 위 히스토그램만으로는 사과와 파인애플을 구분하기가 쉽지 않습니다. 따라서 픽셀별 평균값을 계산해 비교합니다.

fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].bar(range(10000), np.mean(apple, axis=0))
axs[1].bar(range(10000), np.mean(pineapple, axis=0))
axs[2].bar(range(10000), np.mean(banana, axis=0))
plt.show()

평균값과 가까운 사진 고르기

abs_diff = np.abs(fruits - apple_mean)
abs_mean = np.mean(abs_diff, axis=(1, 2))

• 비슷한 샘플끼리 그룹으로 모으는 작업을 군집이라고 합니다.
• 군집은 대표적인 비지도 학습 작업 중 하나이며, 군집 알고리즘에서 만든 그룹을 클러스터라고 부릅니다.

k-평균

• 실제 데이터에서 타깃값을 알고 있지 않은 경우에도 평균을 계산할 수 있어야 합니다.
• 이 경우 k-평균 군집 알고리즘을 사용하고, 이 평균값이 클러스터의 중심에 위치하기 때문에 클러스터 중심 또는 센트로이드라고 부릅니다.

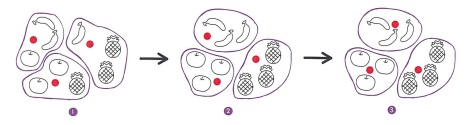
k-평균 알고리즘 소개

• k-평균 알고리즘을 그림으로 간단히 나타내면 다음과 같습니다.

KMeans 클래스

from sklearn.cluster import KMeans
km = KMeans(n_cluster=3, random_state=42)
km.fit(fruits_2d)

클러스터 중심

• KMeans 클래스가 최종적으로 찾은 클러스터 중심은 cluster_centers_ 속성에 저장되어 있습니다.

draw_fruits(km.cluster_centers_.reshape(-1, 100, 100), ratio=3)

최적의 k 찾기

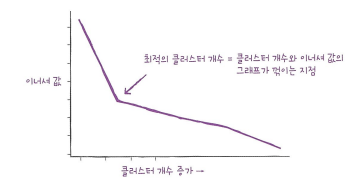
• k-평균 알고리즘은 클러스터 중심과 클러스터에 속한 샘플 사이의 거리를 잴 수 있고, 이 거리의 제곱 합을 이너셔라고 부릅니다.
• 엘보우 방법은 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수를 찾는 방법입니다.

주성분 분석

차원과 차원 축소

• 과일 사진의 경우 10000개의 픽셀이 있기 때문에 10000개의 특성이 있는 셈이고, 이런 특성을 차원이라고도 부릅니다.
• 결국 이 차원을 줄일 수 있다면 저장 공간을 크게 절약할 수 있을 것입니다.
• 비지도 학습의 차원 축소 알고리즘 중 하나로 주성분 분석(PCA)가 있습니다.

PCA 클래스

import numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)

from sklearn.decomposition import PCA
pca = PCA(n_components=50)
pca.fit(fruits_2d)

draw_fruits(pca.components_.reshape(-1, 100, 100))

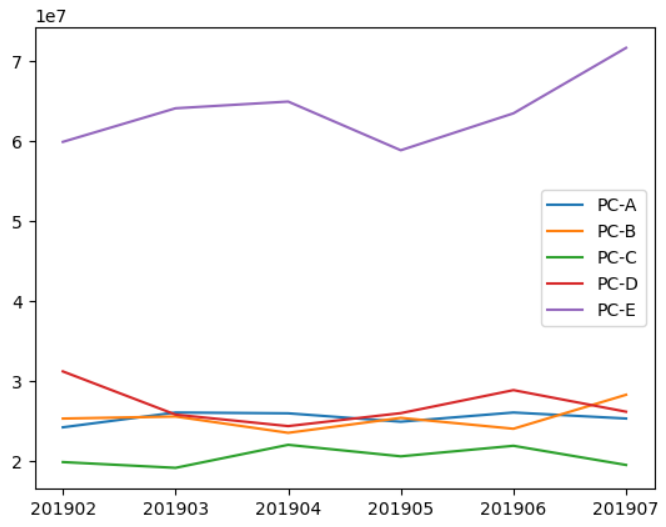
설명된 분산

• 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값을 의미합니다.

plt.plot(pca.explained_variance_ratio_)