물류의 최적 경로를 컨설팅하는 테크닉 10
| No. | 파일 이름 | 개요 |
|---|
| 1 | tbl_factory.csv | 생산 공장 데이터 |
| 2 | tbl_warehouse.csv | 창고 데이터 |
| 3 | rel_cost.csv | 창고와 공장 간의 운송 비용 |
| 4 | tbl_transaction.csv | 2019년의 공장으로의 부품 운송 실적 |
물류 데이터를 불러오자
1
2
3
4
5
6
7
8
9
10
11
| import pandas as pd
factories = pd.read_csv('data/chap06/tbl_factory.csv', index_col=0)
factories
warehouses = pd.read_csv('data/chap06/tbl_warehouse.csv', index_col=0)
cost = pd.read_csv('data/chap06/rel_cost.csv', index_col=0)
cost.head()
trans = pd.read_csv('data/chap06/tbl_transaction.csv', index_col=0)
trans.head()
|
- 처음 데이터를 불러온 후, 데이터의 구조를 확인합니다.
공장 데이터 FCID와 창고 데이터 WHID는 비용 데이터나 운송 실적 데이터에도 있는 것으로 보아 이것이 키인 것을 알 수 있습니다.
- 데이터 분석의 기초가 될 데이터는 운송 실적이기 때문에 이것을 중심으로 각 정보를 결합합니다. ```python
아래와 같이 2개 이상의 키들의 쌍을 기준으로 결합을 수행할 수 있다.
join_data = pd.merge(trans, cost, left_on=[‘ToFC’, ‘FromWH’], right_on=[‘FCID’, ‘WHID’], how=’left’) join_data.head()
join_data = pd.merge(join_data, factories, left_on=’ToFC’, right_on=’FCID’, how=’left’) join_data.head()
join_data = pd.merge(join_data, warehouses, left_on=’FromWH’, right_on=’WHID’, how=’left’) join_data = join_data[[‘TransactionDate’, ‘Quantity’, ‘Cost’, ‘ToFC’, ‘FCName’, ‘FCDemand’, ‘FromWH’, ‘WHName’, ‘WHSupply’, ‘WHRegion’]] join_data.head()
1
2
3
4
5
6
7
8
9
|
* 북부지사와 남부지사의 데이터를 비교하기 위해 각각 해당하는 데이터만 추출해서 변수에 저장합니다.
```python
north = join_data.loc[join_data['WHRegion']=='북부']
north.head()
south = join_data.loc[join_data['WHRegion']=='남부']
south.head()
|
현재 운송량과 비용을 확인해 보자
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| # 1년간의 운송 비용 계산
print('북부지사 총비용: ' + str(north['Cost'].sum()) + '만원') # 북부지사 총비용: 2189.3만원
print('남부지사 총비용: ' + str(south['Cost'].sum()) + '만원') # 남부지사 총비용: 2062.0만원
# 1년간의 운송 총 부품 수 계산
print('북부지사 총부품 운송개수: ' + str(north['Quantity'].sum()) + '개') # 북부지사 총부품 운송개수: 49146개
print('남부지사 총부품 운송개수: ' + str(south['Quantity'].sum()) + '개') # 남부지사 총부품 운송개수: 50214개
tmp = (north['Cost'].sum() / north['Quantity'].sum()) * 10000
print('북부지사의 부품 1개당 운송 비용: ' + str(int(tmp)) + '원') # 북부지사의 부품 1개당 운송 비용: 445원
tmp = (south['Cost'].sum() / south['Quantity'].sum()) * 10000
print('남부지사의 부품 1개당 운송 비용: ' + str(int(tmp)) + '원') # 남부지사의 부품 1개당 운송 비용: 410원
# 단위가 (원)이 아니라 (만원)이 되어야 하는 거 아님?
cost_chk = pd.merge(cost, factories, on='FCID', how='left')
print('북부지사의 평균 운송 비용: ' + str(cost_chk['Cost'].loc[cost_chk['FCRegion']=='북부'].mean()) + '원') # 북부지사의 평균 운송 비용: 1.075원
print('남부지사의 평균 운송 비용: ' + str(cost_chk['Cost'].loc[cost_chk['FCRegion']=='남부'].mean()) + '원') # 남부지사의 평균 운송 비용: 1.05원
|
네트워크를 가시화해 보자
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
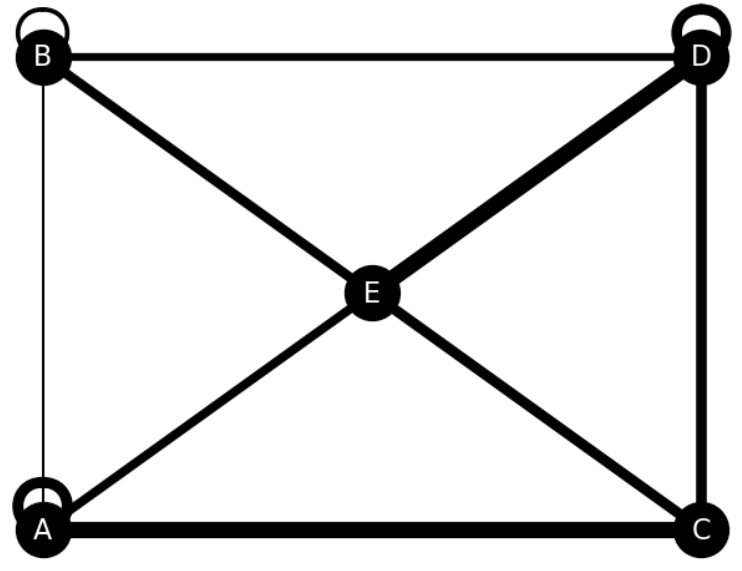
| import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
G.add_node('nodeA')
G.add_node('nodeB')
G.add_node('nodeC')
G.add_edge('nodeA', 'nodeB')
G.add_edge('nodeA', 'nodeC')
G.add_edge('nodeB', 'nodeC')
pos={}
pos['nodeA']=(0,0)
pos['nodeB']=(1,1)
pos['nodeC']=(0,1)
nx.draw(G, pos)
plt.show()
|
- 네트워크를 가시화하면 숫자만으로 알기 어려운 물류의 쏠림과 같은 전체 그림을 파악할 수 있습니다.
네트워크에 노드를 추가해 보자
1
2
3
4
5
6
7
| G.add_node('nodeD')
G.add_edge('nodeA', 'nodeD')
pos['nodeD']=(1,0)
nx.draw(G, pos, with_labels=True)
|
경로에 가중치를 부여하자
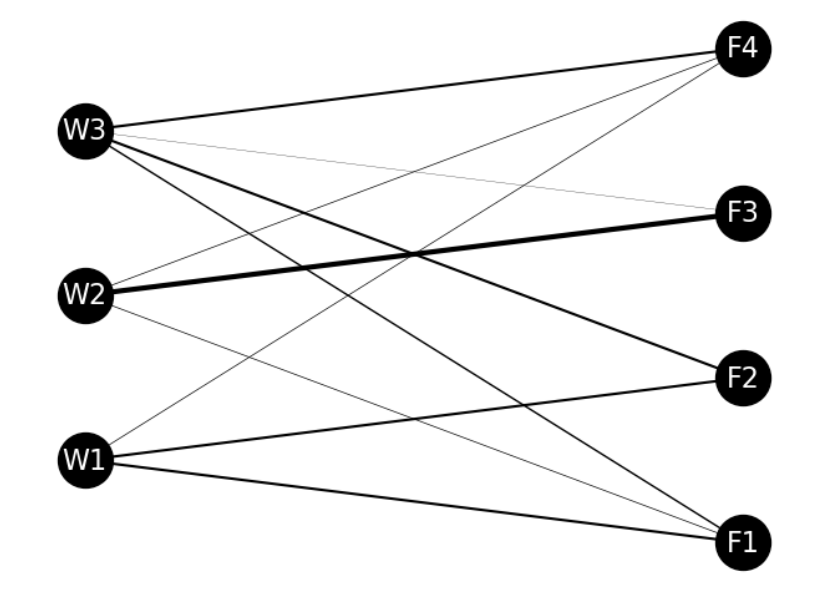
- 가중치를 이용해서 노드 사이의 엣지 굵기를 바꾸면 물류의 최적 경로를 알기 쉽게 가시화할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| df_w.iloc[0][1]
size=10
edge_weights = []
for i in range(len(df_w)):
for j in range(len(df_w.columns)):
edge_weights.append(df_w.iloc[i][j]*size)
G = nx.Graph()
for i in range(len(df_w.columns)):
for j in range(len(df_w.columns)):
G.add_edge(df_w.columns[i], df_w.columns[j])
pos = {}
for i in range(len(df_w.columns)):
node = df_w.columns[i]
pos[node] = (df_p[node][0], df_p[node][1])
nx.draw(G, pos, with_labels=True, font_size=16, node_size=1000, node_color='k', font_color='w', width=edge_weights)
plt.show()
|
- 엣지의 가중치 순서는 나중에 등록할 엣지의 순서와 동일해야 합니다.
운송 경로 정보를 불러오자
| No. | 파일 이름 | 개요 |
|---|
| 1 | trans_route.csv | 운송 경로 |
| 2 | trans_route_pos.csv | 창고 및 공장의 위치 정보 |
| 3 | trans_cost.csv | 창고와 공장 간의 운송 비용 |
| 4 | demand.csv | 공장의 제품 생산량에 대한 수요 |
| 5 | supply.csv | 창고가 공급 가능한 최대 부품 수 |
| 6 | trans_route_new.csv | 새로 설계한 운송 경로 |
1
2
3
| import pandas as pd
df_tr = pd.read_csv('data/chap06/trans_route.csv', index_col='공장')
df_tr.head()
|
운송 경로 정보로 네트워크를 가시화해 보자
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| import pandas as pd
import matplotlib.pyplot as plt
import networkx as nx
df_tr = pd.read_csv('data/chap06/trans_route.csv', index_col='공장')
df_pos = pd.read_csv('data/chap06/trans_route_pos.csv')
G = nx.Graph()
# 노드 설정
for i in range(len(df_pos.columns)):
G.add_node(df_pos.columns[i])
# 엣지 설정 및 가중치 리스트화
num_pre = 0
edge_weights = []
size = 0.1
for i in range(len(df_pos.columns)):
for j in range(len(df_pos.columns)):
if not (i==j):
# 엣지 추가
G.add_edge(df_pos.columns[i],df_pos.columns[j])
# 엣지 가중치 추가
if num_pre<len(G.edges):
num_pre = len(G.edges)
weight = 0
if (df_pos.columns[i] in df_tr.columns)and(df_pos.columns[j] in df_tr.index):
if df_tr[df_pos.columns[i]][df_pos.columns[j]]:
weight = df_tr[df_pos.columns[i]][df_pos.columns[j]]*size
elif(df_pos.columns[j] in df_tr.columns)and(df_pos.columns[i] in df_tr.index):
if df_tr[df_pos.columns[j]][df_pos.columns[i]]:
weight = df_tr[df_pos.columns[j]][df_pos.columns[i]]*size
edge_weights.append(weight)
# 좌표 설정
pos = {}
for i in range(len(df_pos.columns)):
node = df_pos.columns[i]
pos[node] = (df_pos[node][0],df_pos[node][1])
# 그리기
nx.draw(G, pos, with_labels=True,font_size=16, node_size = 1000, node_color='k', font_color='w', width=edge_weights)
# 표시
plt.show()
|
운송 비용 함수를 작성하자
- 최소화 또는 최대화하고 싶은 것을 함수로 정의하는 데, 이것을 목적 함수라고 합니다.
- 다음으로 최소화 또는 최대화를 함에 있어서 지켜야 할 조건인 제약 조건을 정의합니다.
- 즉, 생각할 수 있는 여러 가지 운송 경로의 조합 중에서 제약 조건을 만족시키면서 목적함수를 최소화 또는 최대화하는 조합을 선택하는 것이 최적화 문제의 큰 흐름입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
| import pandas as pd
df_tr = pd.read_csv('data/chap06/trans_route.csv', index_col='공장') # 운송량
df_tc = pd.read_csv('data/chap06/trans_cost.csv', index_col='공장') # 운송 비용
def trans_cost(df_tr, df_tc):
cost = 0
for i in range(len(df_tc.index)):
for j in range(len(df_tr.columns)):
cost += df_tr.iloc[i][j] * df_tc.iloc[i][j]
return cost
print('총 운송 비용: ' + str(trans_cost(df_tr, df_tc))) # 1493
|
- 가설:
운송 비용을 낮출 효율적인 운송 경로가 존재한다. - 위 가설을 입증하고 운송 경로를 최적화하기 위해 먼저 운송 비용을 계산할 함수를 작성하고, 그것을 목적함수로 정의합니다.
- 운송 비용 = 운송량 * 비용
제약 조건을 만들어보자
- 각 창고는 공급 가능한 부품 수에 제한이 있고, 각 공장은 채워야 할 최소한의 제품 제조량이 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| import pandas as pd
df_tr = pd.read_csv('data/chap06/trans_route.csv', index_col='공장')
df_demand = pd.read_csv('data/chap06/demand.csv')
df_supply = pd.read_csv('data/chap06/supply.csv')
# 수요측 제약 조건
for i in range(len(df_demand.columns)):
temp_sum = sum(df_tr[df_demand.columns[i]]) # 해당 공장으로 운송되는 운송량
print(str(df_demand.columns[i])+'으로 운송량: '+str(temp_sum)+' (수요량: '+str(df_demand.iloc[0][i])+')')
if temp_sum>=df_demand.iloc[0][i]:
print('수요량을 만족시키고 있음')
else:
print('수요량을 만족시키지 못하고 있음. 운송경로 재계산 필요')
# 공급측 제약 조건
for i in range(len(df_supply.columns)):
temp_sum = sum(df_tr.loc[df_supply.columns[i]])
print(str(df_supply.columns[i])+'부터의 운송량: '+str(temp_sum)+' (공급한계: '+str(df_supply.iloc[0][i])+')')
if temp_sum<=df_supply.iloc[0][i]:
print('공급한계 범위 내')
else:
print('공급한계 초과. 운송경로 재계산 필요')
|
- 공장의 부품 수요량과 창고의 공급 한계량에 대해서 제약 조건을 만족시키는지 전부 조사합니다.
운송 경로를 변경해서 운송 비용 함수의 변화를 확인하자
- 목적 함수와 제약 조건을 미리 정의해두면, 체계적으로 개선할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| import pandas as pd
import numpy as np
df_tr_new = pd.read_csv('data/chap06/trans_route_new.csv', index_col='공장')
print(df_tr_new)
# 총 운송 비용 재계산
print('총 운송 비용(변경 후) : '+ str(trans_cost(df_tr_new, df_tc)))
# 제약 조건 계산 함수
# 수요측
def condition_demand(df_tr, df_demand):
flag = np.zeros(len(df_demand.columns))
for i in range(len(df_demand.columns)):
temp_sum = sum(df_tr[df_demand.columns[i]]) # 공급량
if (temp_sum>=df_demand.iloc[0][i]):
flag[i] = 1
return flag
# 공급측
def condition_supply(df_tr, df_supply):
flag = np.zeros(len(df_supply.columns))
for i in range(len(df_supply.columns)):
temp_sum = sum(df_tr.loc[df_supply.columns[i]]) # 공급량
if temp_sum<=df_supply.iloc[0][i]:
flag[i] = 1
return flag
print('수요조건 계산결과: '+ str(condition_demand(df_tr_new, df_demand)))
print('공급조건 계산결과: '+ str(condition_supply(df_tr_new, df_supply)))
|
- 이번에 읽어 들인 경로는
W1에서 F4로의 운송을 줄이고, 그만큼을 W2에서 F4로의 운송으로 보충하는 것입니다. - 이것에 의해 운송 비용은 1428로, 원래 운송 비용 1493과 비교하면 약간의 비용 절감을 기대할 수 있습니다.
- 그렇지만 두 번째 공급 조건을 만족시키지 못해 공장
W2의 공급 한계를 넘어버린 것을 알 수 있습니다. - 모든 제약 조건을 만족하면서 비용 절감을 하는 것은 그렇게 간단하지 않다는 것을 알 수 있습니다.