9.22 Chapter 04

추론통계 ~ 신뢰구간

추론통계를 배우기 전에

전수조사와 표본조사

• 알고자 하는 대상인 모집단을 알아보고자 사용했던 2가지 방법
  1. 전수조사: 기술통계 방법을 사용
  2. 표본조사: 추론통계 방법을 사용

데이터를 얻는다는 것

• 데이터(표본)을 얻는다는 것은 무엇인가?
• 모집단에 포함된 전체 값으로 구성된 분포에서 일부를 추출하는 것
• 모집단을 나타내는 분포: 모집단 분포

• 모집단 분포를 특징 짓는 양을 모수 또는 파라미터라 부릅니다.

• 확률 분포와 실현값의 관계는 모집단과 표본의 관계와 매우 비슷하다.
• 지금부터는 모집단=확률분포, 표본=확률분포를 따르는 실현값이라 생각합시다.
• 즉, 얻은 표본으로 모집단을 추정한다.라는 원래 목표를 얻은 실현값으로 이 값을 발생시킨 확률분포를 추정한다.라는 목표로 바꾸어 말할 수 있습니다.
• 수학적인 확률분포로 모집단 분포를 근사하는 것을, 여기서는 모형화(modeling)라 부르도록 합시다.

---

• 모집단에서 표본을 얻을 때 중요한 것이 무작위 추출(random sampling)입니다.
• 이는 데이터를 얻을 때 모집단에 포함된 요소를 하나씩 무작위로 선택하여 추출하는 방식입니다.
  1. 단순무작위추출법
• 가장 이상적인 무작위추출 방법으로 표본에 있을 수 있는 모든 요소를 목록으로 만들고, 난수를 이용하여 표본을 정하는 것입니다.
  1. 층화추출법
• 모집단을 몇 개의 층(집단)으로 미리 나눈 뒤, 각 층에서 필요한 수의 조사대상을 무작위로 추출하는 방법입니다.
• 이 외에도 계통추출법, 군집추출법 등 다양한 방법이 존재합니다.
• 모집단에 대해 추정한 결과를 어느 정도 일반화할 수 있는가는, 각 분야 고유의 지식(도메인 지식)에 따라 달라집니다.

추론통계를 직감적으로 이해하기

• 시사점 1: 정말로 알고자 하는 것은 표본 데이터가 아니라 모집단이다.
• 시사점 2: 모집단의 모든 요소를 다 조사하는 전수조사는 어렵다.
• 시사점 3: 작은 크기의 표본으로도 모집단을 추론할 수 있다.
• 시사점 4: 표본을 추출할 때는 무작위로 추출해야 한다.

표본오차와 신뢰구간

모집단과 데이터 사이의 오차 고려하기

• 정말로 알고 싶은 것 = 모집단평균 μ
• 모집단을 직접 알 수는 없으므로 모집단의 일부인 크기 n인 표본을 모집단에서 무작위로 추출하여, 이 표본에서 모집단평균 μ를 추정하는 것으로 생각해 가겠습니다.

표본오차

• 정말로 알고 싶은 것(모집단 평균)과 실제로 손 안에 있는 데이터(표본 평균)에는 어긋남(오차)이 생기는 것입니다.

• 이런 어긋남을 표본오차(표집오차, sampling error)라 합니다.

• 표본오차는 확률적으로 바뀐다.

---

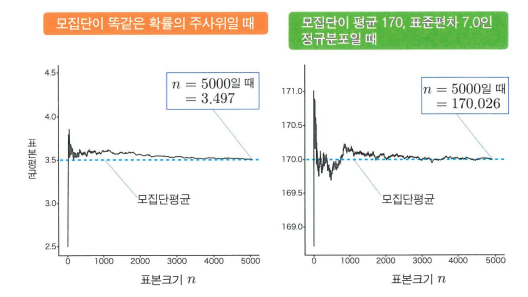
• 큰 수의 법칙
• 표본 평균과 모집단 평균의 관계에는 큰 수의 법칙이 성립합니다.
• 이는 표본크기 n이 커질 수록 표본 평균이 모집단 평균에 한없이 가까워진다는 법칙입니다.
• 다른 말로 하면, 표본 오차가 0에 한없이 가까워진다는 뜻이기도 합니다.

표본오차의 확률분포

• 표본오차의 확률분포를 알면 어느 정도 크기의 오차가, 어느 정도의 확률로 나타나는지를 알 수 있게 됩니다.

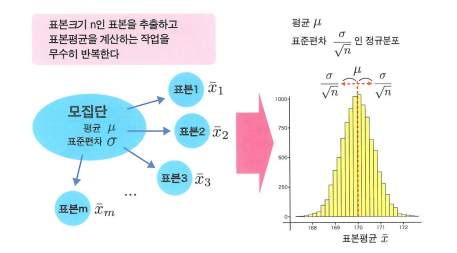
• 표본오차의 분포에 관해 중요한 정보를 제공하는 것이 중심극한정리입니다.
• 이는 모집단이 어떤 분포이든 간에, 표본 크기 n이 커질수록 표본평균의 분포는 정규분포로 근사할 수 있다는 것을 의미합니다.
• 표본 평균의 분포에 대해서, 평균은 모집단 평균 μ, 표준편차는 모집단의 표준편차 σ와 표본 크기 n을 이용하여 σ/√n 로 나타냅니다.

---

• 모집단의 성질을 추정하는 데 사용하는 통계량을 추정량이라 합니다.
• 표본크기 n을 무한대로 했을 때, 모집단의 성질과 일치하는 추정량을 일치추정량이라 하고, 추정량의 평균값(기댓값)이 모집단의 성질과 일치할 때의 추정량은 비편향추정량이라 합니다.
• 표본표준편차를 계산 시, 올바르게는 n-1로 나눈 다음 식이 모집단 표준편차 σ의 비편향추정량이 됩니다.

• 이는 표본변수, 표본평균, 모평균의 위치관계를 바탕으로 표본평균을 기반으로 표준편차를 계산했을 때의 작은 값이 되는 것(과소평가)을 보정하고자 함입니다.

• σ/√n을 표준오차(standard error)라고 합니다.

신뢰구간이란?

• ~% 신뢰구간을 해석하면 "~%의 확률로 이 구간에 모집단평균 μ가 있다."가 됩니다.
• 신뢰구간은 표본에서 구한 모집단 μ의 추정값을 어느 정도 신뢰할 수 있는지를 나타낸다고 할 수 있습니다.

t분포와 95% 신뢰구간

• 중심극한정리는 표본크기 n이 커질수록 근사적으로 성립하기 때문에, 실제 데이터 분석에서 볼 수 있는 작은 표본크기의 경우 표본오차가 정규분포를 따른다고 말할 수 없습니다.
• 또한 모집단의 σ대신 s를 써야만 합니다.
• 이를 위해 작은 표본으로 모집단 전체를 추정하고자 t분포가 고안되었습니다.
• t분포는 모집단이 정규분포라는 가정하에 미지의 모집단 표준편차 σ를 표본으로 계산한 비편향표준편차 s로 대용했을 때, 편차를 표준오차로 나누어 표준화한 값이 따르는 분포입니다.