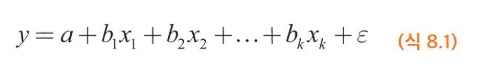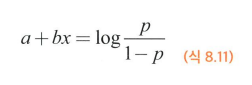11.21 Chapter 8-9

통계 모형화

선형회귀 원리와 확장

선형회귀는 다양한 해석 방법의 기초

• 확장 방향성은 크게 설명변수의 개수를 늘리거나 유형 변경하기, 반응변수의 유형 변경하기, 회귀모형의 형태 변경하기 등 3가지로 나눌 수 있습니다.

다중회귀

• 설명변수가 1개인 것을 단순회귀라 하고, 설명변수가 여러 개인 것을 다중회귀라 합니다.
• 설명변수가 k개인 가장 단순한 다중선형회귀모형은 다음과 같이 쓸 수 있습니다.
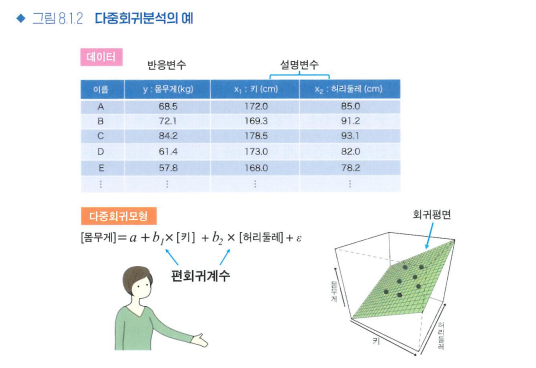
• 아래의 그림에서 기울기 b1, b2를 다중 회귀에서는 편회귀계수라 부릅니다.
• 설명변수가 2개일 때 그래프를 그리면 회귀모형은 직선이 아닌 평면이 되는데, 이를 회귀평면이라 합니다.

• 아래의 그림은 다중 회귀의 결과를 나타낸 그림입니다.
• 아래의 표에서 주목해야 할 점은 추정된 편회귀계수와 그 유의성입니다.
• 또한 R^2값과 마지막의 F통계량에서 얻은 p값에도 주목해야 하는데, 편회귀계수가 모두 0인 모형을 귀무가설로 하여, 회귀모형의 설명력의 유의성을 조사합니다.

편회귀계수

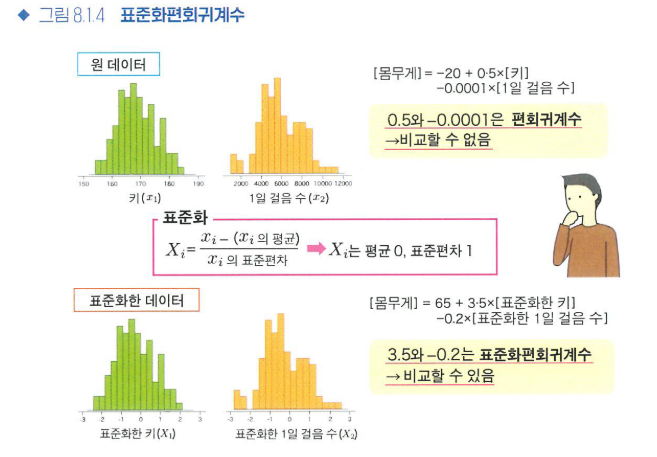
• 회귀분석에서 구한 편회귀계수는 설명변수의 데이터 퍼짐 정도나 단위에 따라 크게 달라지기 때문에 편회귀계수끼리 비교할 수는 없습니다.
• 편회귀계수를 비교하기 위해 표준화편회귀계수를 이용합니다.
• 표준화편회귀계수는 회귀분석을 시행하기 전에 각각의 설명변수를 평균 0, 표준편차 1로 변환한 다음, 회귀분석을 시행하여 구한 회귀계수입니다.
• 상관계수가 1에 가까운 강한 상관이 있을 때는, 뒤에 설명할 다중공선성이 있는지를 의심하고 이에 대처해야 합니다.

범주형 변수를 설명변수로

• 범주에는 대소 관계가 없으므로, 회귀분석의 설명변수로 이용할 때는 0 또는 1과 같은 가변수를 설명변수로 이용하는 등의 요령이 필요합니다.

공분산분석

• 분산분석의 해석 정밀도를 향상시키는 공분산분석을 설명합니다.
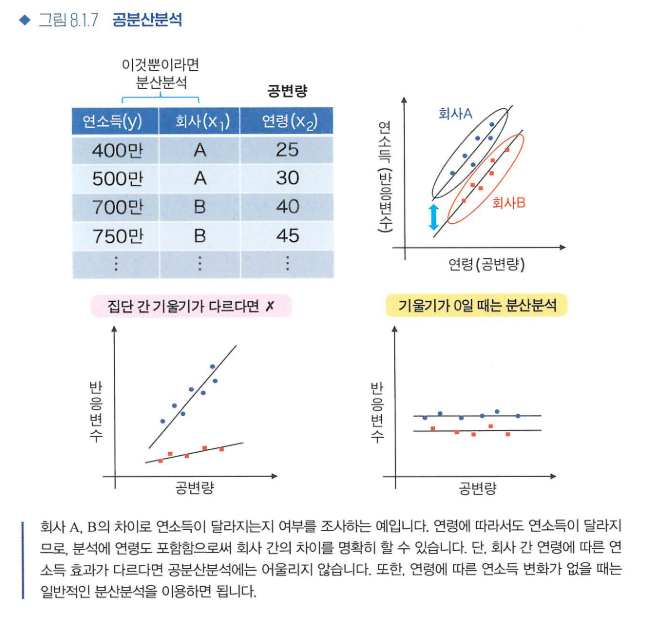
• 일반적인 분산분석에 사용하는 데이터와 함께 양적 변수 데이터가 있는 경우에 후보가 되는 방법입니다.

• 이 새로 추가한 양적 변수를 공변량이라 합니다.

• 공분산분석의 사용 조건은 다음과 같습니다.
  1. 집단 간 회귀의 기울기가 서로 다르지 않을 것입니다.
  2. 회귀계수가 0이 아니어야 합니다.

고차원 데이터 문제

• 차원이 늘어날수록 파라미터 추정에 필요한 데이터 양이 폭발적으로 증가한다는 문제가 있습니다.
• 이를 차원의 저주라고 합니다.
• 차원이 증가할수록 다중공선성 문제가 일어나기 쉬우므로, 모형의 추정 정밀도가 떨어지고 맙니다.
• 즉, 이에 대한 대책으로 차원축소 방법을 이용하여 차원을 줄일 수 있습니다.

다중공선성

• 설명변수가 여러 개인 다중회귀에서 설명변수 사이에 강한 상관이 있는 경우, 다중공선성이 있다고 말합니다.
• 다중공선성 정도를 측정하려면, 먼저 분산팽창인수 VIF를 계산합니다.
• VIF 값은 각 설명변수마다 산출됩니다.
• VIF>10 이라면, 2개 사이의 상관이 아주 강한 것입니다.
• 다중공선성이 강하다고 판단했을 때는, 서로 상관이 있는 2개 변수 중 하나를 없애거나, 주성분분석 등의 차원 축소 방법을 이용하여 설명변수의 개수를 줄이는 것이 좋습니다.

회귀 모형의 형태 바꾸기

상호작용

• 설명변수 간의 상승효과를 상호작용이라 하며, 선형회귀모형안에서 곱셈식으로 도입할 수 있습니다.

이원배치 분산분석

• 하나의 요인만 다루므로 일원배치 분산분석이라 합니다.
• 분산분석에서도 이와 마찬가지로 여러 개의 요인을 동시에 고려할 수 있는데, 이를 다원배치 분산분석이라 합니다.
• 이 중 2개의 요인이 있는 이원배치 분산분석을 설명하겠습니다.
• 가설검정 결과 상호작용항 c1이 유의미하지 않다면 상호작용이 없다고 보고, 각각의 주효과를 그대로 평가합니다.

비선형회귀

• x에 관해 비선형인 모형을 데이터에 적용할 수는 있으나, 주의가 필요합니다.
• 가령 2차 함수를 적용한 경우에는 그 계수의 해석이 어려워지기 때문에, 무턱대로 복잡한 모형을 채택하는 것은 통상 바람직하지 않습니다.
• 또한, 2차 함수뿐 아니라 3차 함수나 10차 함수 같은 후보도 얼마든지 있으므로, 어느 모형이 적절한가, 애당초 적절이한 말은 어떤 관점에서 본 적절함인가를 생각해야 합니다.

일반화선형모형의 개념

선형회귀 원리 확장하기

• 설명변수가 양적 변수인 다중회귀부터 설명변수가 범주형 변수인 분산분석까지를 포괄하는 것을 일반선형모형이라 합니다.
• 최소제곱법이 아닌 확률분포에 기반한 최대가능도 방법으로 회귀모형을 추정하는 방법을 일반화선형모형이라 합니다.
• 또한 데이터의 성질을 고려하면서 확률 모형을 가정하고, 파라미터를 추정하여 모형을 평가하는 일련의 작업을 가리키며 통계 모형화라고 부릅니다.
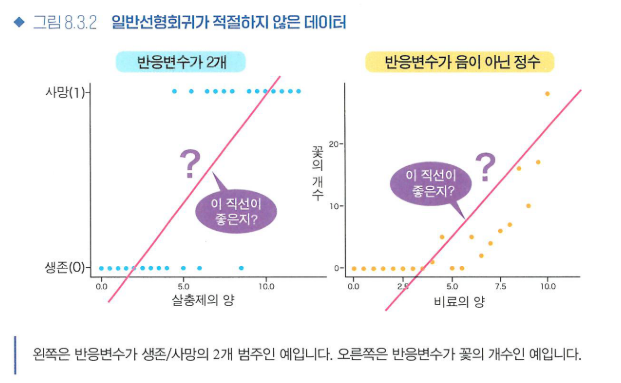
• 또한 실제 데이터 해석에서 반응변수가 예/아니오와 같이 값이 2개인 변수이거나, 물건이나 생물의 수처럼 음이 아닌 정수인 상황에서는 선형회귀가 적절하지 않습니다.
• 따라서 이러한 경우 일반화 선형모형 원리로써 확률분포를 적절하게 고려해 모형화할 필요가 있습니다.

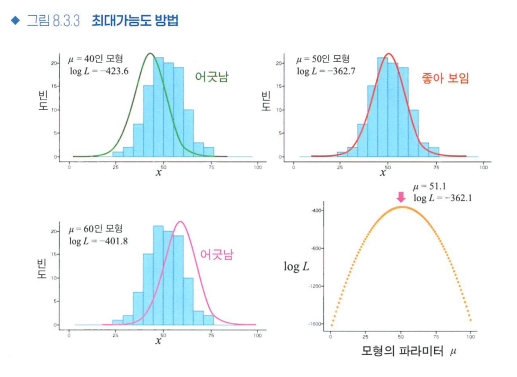
가능도와 최대가능도 방법

• 위의 식에서 P를 데이터 x에 대한 파라미터의 함수로 보고 가능도라고 합니다.
• 가능도가 크다는 것은, 그 파라미터에서 얻은 데이터가 나타나기 쉽다는 뜻입니다.
• 이렇게 가능도를 최대화하며 이를 추정값으로 삼으면 얻은 데이터에 가장 잘 들어맞는 파라미터를 정할 수 있습니다.
• 이를 최대 가능도 방법 또는 최대 가능도 추정 이라 합니다.

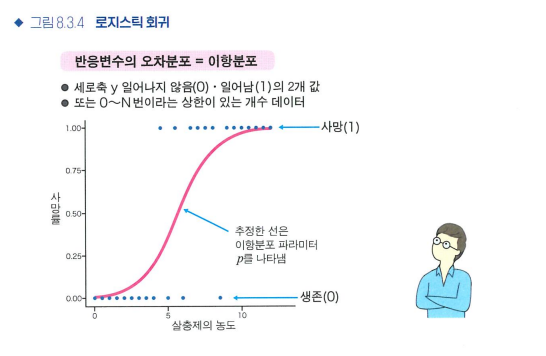
로지스틱 회귀

• 로지스틱 회귀는 반응변수가 값이 2개인 범주형 변수일 때 사용하는 회귀입니다.
• 범주 하나가 일어날 확률을 p로 두고, 설명변수 x가 바뀌었을 때 p가 얼마나 달라지는 지를 조사합니다.

• 로지스틱 회귀에 사용한 이산형 확률분포를 이항분포라고 합니다.
• 아래의 우변을 로짓 함수라고 부르며, 일반화선형모형에서 좌변을 선형예측변수라고 하며, 선형예측변수와 반응변수의 확률분포 파라미터를 잇는 함수를 연결함수라 합니다.

푸아송 회귀

• 데이터가 음수가 되지 않는 정수일 때, 특히 반응변수가 개수인 경우 고려해볼 수 있는 일반화 선형모형이 바로 푸아송 회귀입니다.
• 푸아송 분포란 낮은 확률로 일어나는 무작위 사건에 대해, 평균이 i번일 때 몇 번 일어나는지를 나타내는 확률분포입니다.

통계 모형의 평가와 비교

왈드 검정

• 최대가능도 방법으로 얻은 추정값/표준오차를 왈드 통계량이라 합니다.
• 이러한 검정 방법을 왈드 검정이라 합니다.

가능도비 검정

• 가능도비 검정을 시도하기 위해서는 비교할 2개의 모형 중 어느 한쪽이 다른 한쪽을 포함하는 관계여야 합니다.
• 어떤 가정하에 무작위로 데이터를 생성하고 추정량의 성질을 조사하는 방법을 부트스트랩 방법이라 합니다.

가설검정의 주의점

재현성

가설검정, 이해는 어렵지만 시행은 간단

• 이치를 제대로 이해하지 않아도, 선행 연구를 모방하여 가설검정을 시행, p<0.05를 얻기만 하면 그만이라 여기는 사용자가 많다는 실정입니다.
• 이로 인해 재현성 위기라는 중대한 문제가 일어난다고 합니다.

재현성 위기

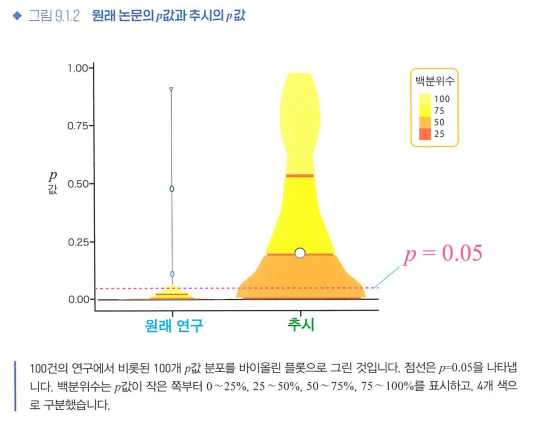
• 재현성이란 누가 언제 어디서 실험하더라도, 조건이 동일하다면 동일한 결과를 얻을 수 있어야 한다는 것입니다.
• 재현성이 없다는 것은 원래 논문의 주장이 잘못되었을 가능성이 있다는 것을 의미합니다.
• 이 문제를 재현성 위기라 합니다.

• 낮은 재현성을 초래하는 또 하나의 주 원인은, 가설검정의 사용 방법에 있다고 여겨집니다.
• 놀랍게도, 가설검정 사용 방법에 따라 p값이 0.05보다 작아지게 조작하는 것이 가능합니다.
• 이렇게 자신에게 유리하도록 p값을 조작하는 행위를 p-해킹이라고 합니다.

가설검정의 문제점

• 가설검정의 원리와 p값을 이해하지 못한 채 사용하는 사람이 많다는 것입니다.

베이즈 인수

• 가설검정에서 귀무가설의 지지와 관련된 문제의 해결책 중 하나로, p값 대신 사용하는 베이즈 인수라는 지표가 있습니다.
• 가설을 수학적으로 나타낸 것을 모형이라 할 때, 어떤 모형 M이 얻은 데이터 x를 설명하는 데 얼마나 적절한지는 주변 가능도 또는 에비던스라는 식으로 나타냅니다.

p-해킹

• p-해킹이란 의도하든, 의도하지 않든 p값을 원하는 방향으로 조작하는 행위입니다.